Système duodécimal
Un système duodécimal est un système de numération de base 12.
Avantages
Un système en base 12 est meilleur que le système décimal tant d’un point de vue mathématique que pour d’autres côtés pratiques. En effet 2, 3, 4, 6 sont des diviseurs de 12, ce qui facilite la mise en fraction. Comparé aux diviseurs 2 et 5 du système décimal, le système duodécimal offre plus de possibilités.
Le fait de compter en base 10 est un “accident biologique”. Il ne fait aucun doute que nous aurions adopté un système en base 12 si nous étions nés avec autant de doigts, et tout aurait été beaucoup plus simple !
Il existe malgré tout une manière efficace de compter sur ses doigts en base 12 : compter les phalanges de la main en omettant celles du pouce (qui est utilisé pour compter les phalanges des autres doigts) :
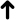Kingsland Camp
En base 12, on utilise les 10 chiffres de 0 à 9, suivis des lettres A et B, respectivement pour 10 et 11 (voir ici), mais le fait d’ajouter deux nouveaux chiffres est une bonne occasion pour créer un nouveau système numéral avec des symboles beaucoup plus cohérents.
Ainsi, Kingsland Camp a proposé un ensemble “idéal” de chiffres dans son article “Number symbols” (The Duodecimal Bulletin, Vol.2, n°1, page 16).
Nous proposons ici l’adoption de ce système en modifiant la valeur des symboles de manière à ce que le 6 soit le chiffre du haut dans un cadran :
La forme de ses symboles était destinée à retranscrire le chiffre qu’ils représentent avec le plus de cohérence possible, par leur orientation rotative :
- Les moitiés sont représentées par {
, 
}, des cercles avec des traits verticaux en leur centre. - Les quarts impairs par {
, 
}, des cercles avec des traits à gauche ou à droite.
Les chiffres représentant la gamme des quarts { 0, 3, 6, 9 } peuvent être lus comme les cadrans d’une horloge: { , , , }.
- La notation de Camp note les tiers par {
, 
}
et la séquence des sixièmes par {, 
, , , , 
}.
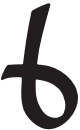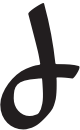Ainsi, tous les chiffres qui représentent un sixième d’une douzaine, et qui ne sont pas déjà pris par les quarts, apparaissent comme un symbole en forme de “poisson”.
- La notation de Camp traite également les autres chiffres impairs { 1, 5, 7, B } d’une manière qui les accentue, avec une forte ouverture angulaire du symbole de manière à ce que celui-ci pointe dans la direction du chiffre sur le cadran d’une horloge standard : {
, 
, 
, 
}
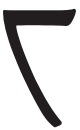Horloge
Voici une proposition idéale d’horloge duodécimale : https://clock.dozenal.ca/clock/diurnal_1
La petite aiguille fait un tour en une journée. Il est minuit lorsqu’elle est sur le 0, et midi lorsqu’elle pointe vers le 6 (analogie avec la position du soleil à cette heure de la journée). Chaque aiguille tourne 12 fois plus vite que la précédente plus courte, donc chaque aiguille fait 1/12e de tour à chaque tour complet de l’aiguille qui la suit.
Il est très facile de lire l’heure : il suffit de lire le chiffre vers lequel pointe les aiguilles. À midi, il est 600. Cela évite de se casser la tête si on veut calculer le temps écoulé entre 11:31:40 et 16:03:20, par exemple.
16:03:20 – 11:31:40 = 4:31:40 ➜ 804 – 592 = 232
Pour éviter les malentendus, il serait important d’appliquer un moyen simple pour indiquer à son interlocuteur si c’est le système décimal ou le système duodécimal qui est utilisé dans la conversation. Je propose d’ajouter le mot “Kamp” (mot issu du nom “Kingsland Camp”) pour préciser que la conversation est en base douze, et ajouter “kon dosa bazo” (“avec base dix”) pour préciser que la conversation est en base dix.
Oui tu as raison. J’avais déjà proposé quelque chose du genre sur l’Atelier.
Je suggérais de préciser la base après chaque nombre, de la même manière que tu ajoutes une unité (mètres, minutes, dollars…), comme ceci :
terunti-bi [baze 10]
terunti-bi [baze 12]
Petite remarque : dos veut dire “dix” en base 12, mais il n’est pas très cohérent d’utiliser dos lorsqu’on parle de base 10 (dans laquelle 10 se dit unti)
Cela dit c’est une bonne remarque, nous devrions la rajouter à la page
Le problème est que lorsque tu écris “terunti-bi [baze 10]” et “terunti-bi [baze 12]”, tu utilises la base dix dans les deux cas pour écrire entre les crochets. Et comment prononcerait-on ce qui est entre crochets ?
Quand en français on parle de base huit, on dit bien : “base huit” alors qu’en base huit, ce nombre se dit “dix”.
Ah oui… tu as encore raison (c’est une mauvaise habitude que tu as là)
mais faut que tu arrêtes parce que tu vas donner raison à Silvano, qui disait qu’il fallait nommer différemment les chiffres selon qu’on utilise la base 10 ou 12 : http://www.ideolangues.org/t2551-duodecimal#69827
La raison pour laquelle je n’étais pas d’accord avec lui, c’est que je n’imagine pas les 2 systèmes coexister, hormis pendant une période de transition relativement courte (comme le passage au système métrique dans les pays anglo-saxons, ou le passage à l’euro en Europe). Pendant cette période, je ne vois pas de problème à utiliser le système décimal comme référence pour indiquer dans quelle base on compte, de manière à ce que les gens s’habituent aux nouvelles valeurs.
Cela dit, tu n’as pas tort, mais le problème avec Camp c’est qu’il ne représente pas le système duodécimal en lui-même, mais juste une manière d’en retranscrire les chiffres. On pourrait très bien utiliser le système duodécimal sans utiliser les symboles de Camp.
As-tu une autre proposition ?
Ma proposition est de dire :
“terunti-bi [baze dos]”
ou “terunti-bi [baze Kamp]” quand il faut préciser.
Pour éviter les malentendus, il serait important d’appliquer un moyen simple pour indiquer à son interlocuteur si c’est le système décimal ou le système duodécimal qui est utilisé dans la conversation. Je propose d’ajouter le mot “Kamp” (mot issu du nom “Kingsland Camp”) pour préciser que la conversation est en base douze, et ajouter “o dosa baze” (“en base dix”) pour préciser que la conversation est en base dix.
Je comprends Djuna quand il dit que “Camp” n’est pas une bonne idée. C’est comme si on disait “cyrillique” pour parler d’alphabet, alors que ce n’est qu’une représentation parmi d’autres.
Moi je propose de faire comme le suggérait Silvano, et d’avoir des chiffres différents selon le système, mais sans être trop radical. Par exemple, on pourrait dire “unti” quand on parle de 10 dans le système décimal, et “unte” pour 10 dans le système duodécimal.
On aurait donc : un, bi, ter, kwar, pe, sis, ta, oc, nof, unti, unti-un, unti-bi… (bazo unti)
et : un, bi, ter, kwar, pe, sis, ta, oc, nof, dos, lef, unte, unte-un, unte-bi… (bazo unte)
Nita, je suis tout à fait d’accord avec toi ! Ton idée est mieux que la mienne !
C’est effectivement une excellente idée !
On va faire comme ça !
Merciii! Je suis contente que vous trouvez ça bien aussi ^^
Le paragraphe sur les nombres premiers ne me parait pas exact, car le nombre 1 n’est pas premier. La série commence par (2; 3; 5; 7; 11). Ainsi votre paragraphe est vrai seulement à partir du nombre 5 (symbole ouvert type 7 écrit symétriquement).
Tu as raison, merci pour la correction !
c est dommage que les symboles proposés pour les chiffres n ont pas en compte la dyslexie.
(les symboles pour les lettres, non plus).
Je ne sais pas quoi répondre, je sais bien peu de choses sur la dyslexie.
Cela dit, j’aurais envie de te répondre que c’est différent dans ce cas-ci, parce que la forme des symboles n’est pas arbitraire.
Ces symboles ne se ressemblent pas comme un d ou un b. La ressemblance est comparable à celle qu’il y a entre ← et →, ↑ et ↓… ce qui me semble quand même assez facile à distinguer (pour moi)
Il me semble que l’un des symptômes de la dyslexie est justement de faire “pivoter” erronément, en tout cas d’avoir du mal à spatialiser, les graphèmes, ce qui induit qu’un , un b voire un q pourront être confondus.
Sinon, c’est une idée prometteuse, les avantages de la base 12 sur celle de 10 étant nombreux dans pas mal de domaines tant pratiques que scientifiques.
Donc on peut bien confondre un ← et un → ?
Bah… De ce que je sais, le degré de sévérité de la dyslexie est influencé par la complexité orthographique d’une langue. Je pense que ça joue en la faveur d’un système qui serait adopté parallèlement au mundeze.